(ITUNES OR LISTEN HERE)
The Free Open Access Medical Education (FOAM)
We cover Dr. Rory Spiegel’s blog EMNERD, covering an article in Chest 2015 by Pivetta et al, discussing the ways lung ultrasound (US) may be far more helpful than the brain natriuretic peptide (BNP) in determining heart failure in the dyspneic patient.
- BNP: + LR 2, – LR 0.2
- Lung US: + LR 22, – LR 0.03
Core Content – Likelihood Ratios
Likelihood Ratios can help us use diagnostic maneuvers to determine whether a patient has a disease process. The calculations (as promised on the podcast):
- + LR = Sensitivity/(1-Specificity)
- -LR = 1- Sensitivity/(Specificity)
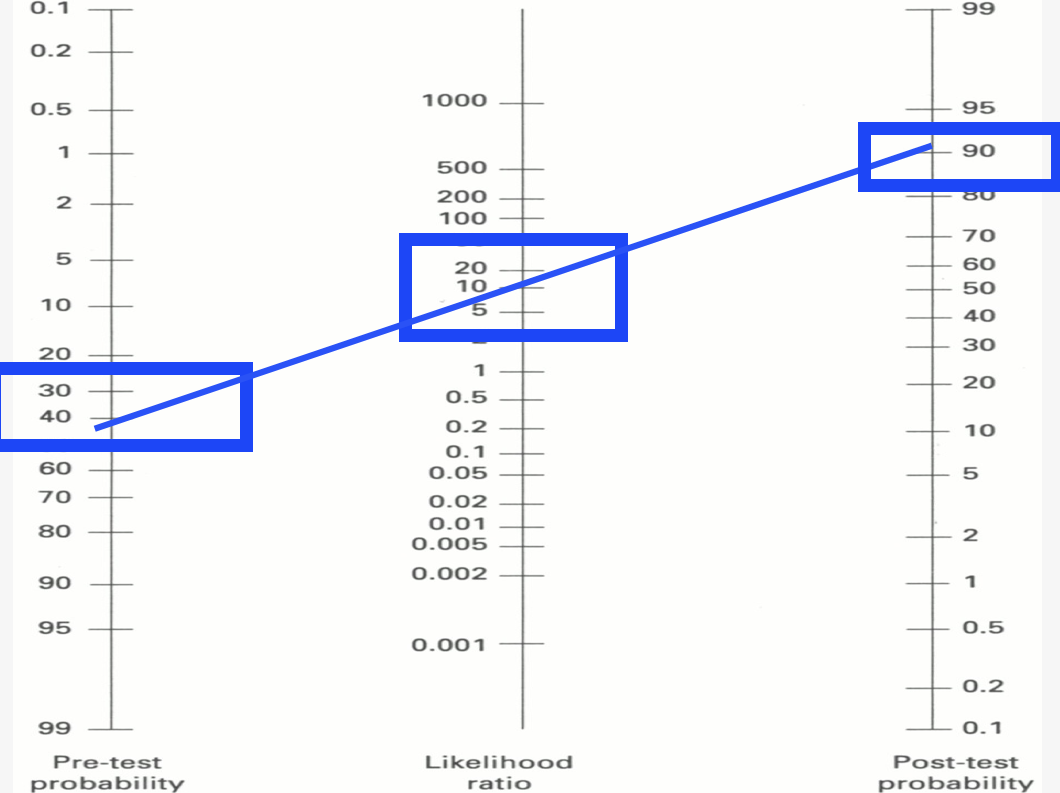
Interpreting LRs really involves only 3 numbers: 1, 10, 0.1.
The utility of likelihood ratios also depends on our pre-test probability. This is essentially our assessment of a patient. Pretend that a patient comes in and states she’s 18 weeks pregnant and she has an intrauterine pregnancy on bedside ultrasound with a fetal heart rate of 150. Your pretest probability that this patient is pregnant is 100%. As such, no test will really be able to move that needle. Similarly, a male comes in with abdominal pain and a normal genital exam. What’s your pre-test probability that the patient is pregnant? Somewhere around 0%. Again, a test will not help you here, regardless of the LR of a pregnancy test. Another 28 year old female patient may come in with abdominal pain and last menstrual cycle 3 weeks ago. What’s your pretest probability that she’s pregnant? Probably in that uncertain but possible range – 20-50%. Here, a test may be useful if it has a good LR. If the +LR of the HCG is high the patient is very likely pregnant and, conversely a low -LR meaning that if the test is negative, the patient is nearly certainly not pregnant.
LR near 1 is useless. Using the Fagan nomogram, one can see that if the pre-test probability is in the “I’m not sure range”, a LR near 1 moves the needle slightly up but to the “I’m still not sure range.” This means that the diagnostic test will not be much help in our post-test probability.
-LRs are helpful once they’re in the 0.1 range. Using this nomogram we can see that in a patient that we’re not sure about, a test with a -LR of 0.1 can reduce the likelihood that the patient has the disease in question to the low single digits (whether or not that’s enough depends on the disease process in question).

+ LRs near 10 are very useful as, if the test is positive, the patient likely has the disease. In a patient that one says “maybe they have X disease?”, a pre-test probability of say, 40%, a positive test with a +LR of 10 means that there’s a 90-something percent probability that the patient does have the disease. We can be much more certain.
+LRs from 0 to 5 are not very useful. They may shift the probability from a pre-test probability of “maybe?” to a post-test probability of “maybe.”
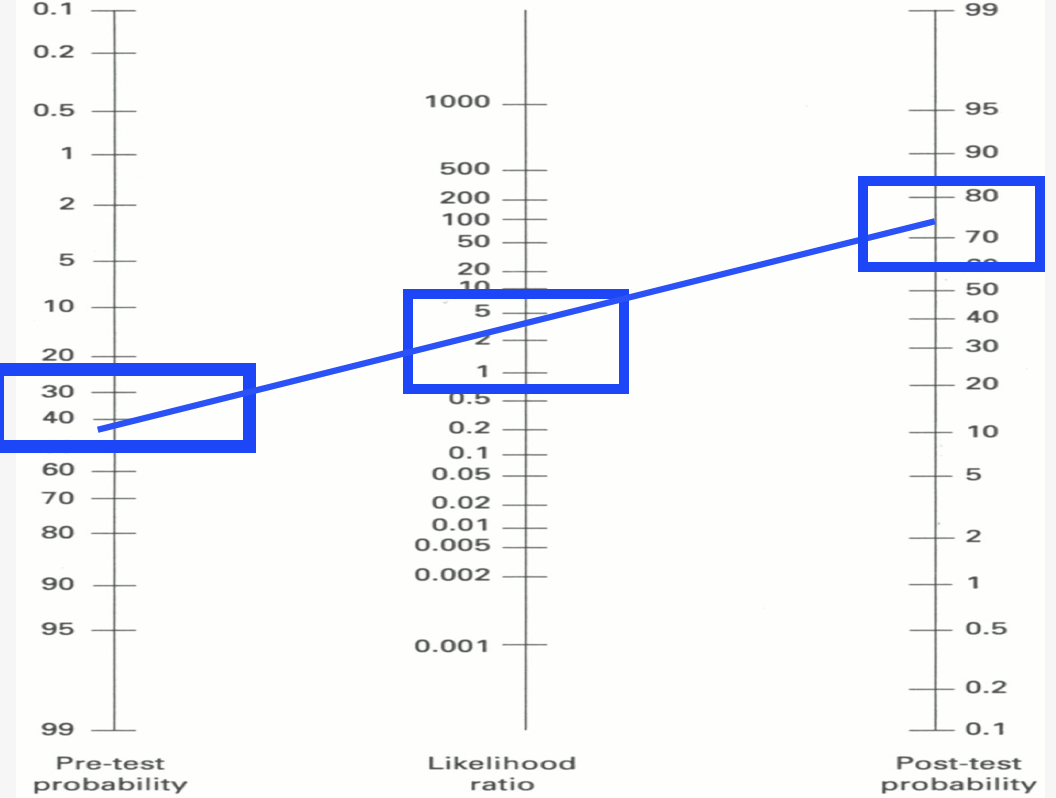
-LRs from 1 to 0.2 are not very useful. They may shift the post-test probability slightly but not much.
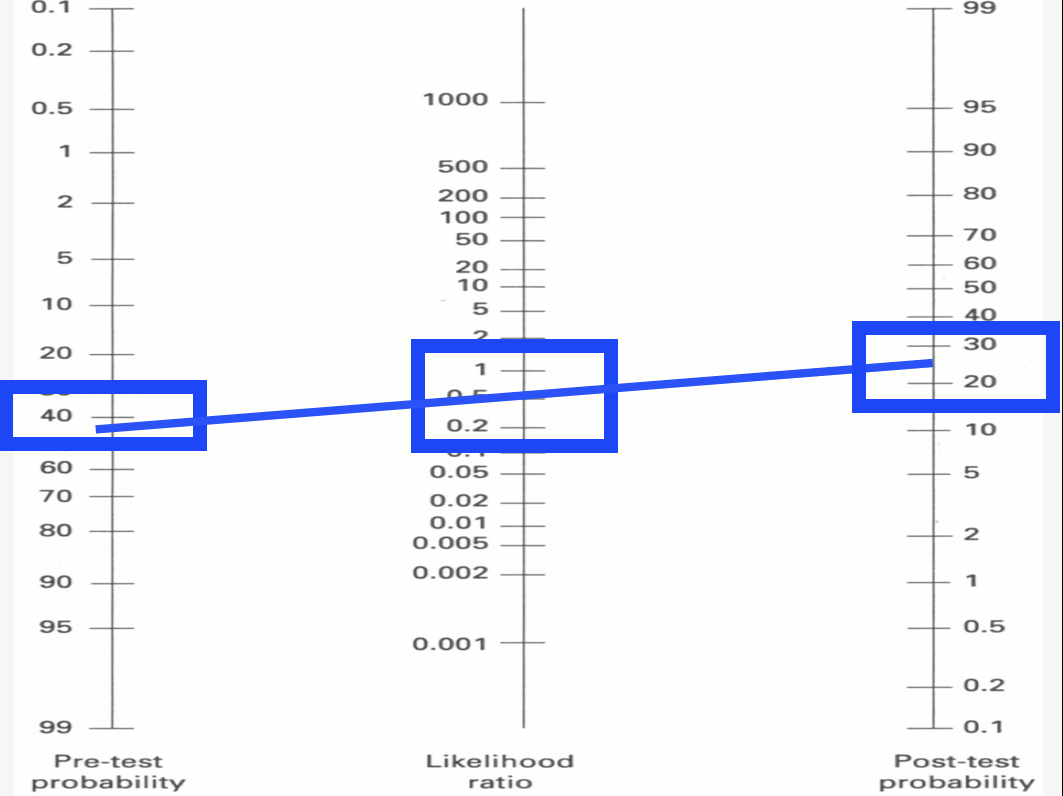
More resources:
Deeks JJ. Diagnostic tests 4: likelihood ratios. BMJ. 329(7458):168-169. 2004. [article]